research method
Based on the aforementioned analysis of reservoir geological characteristics, we first investigated the brittle properties of reservoir rocks in detail and discussed their influence on the volumetric fracturing process. Based on this basis, we further comprehensively analyzed rock mechanics, in-situ stress, and natural crack development to comprehensively understand the main control effects of these factors on volumetric fracturing. Through comprehensive evaluation, we accurately evaluated the feasibility of using volumetric fracturing to create a complex fracture network, providing an essential theoretical basis for subsequent volumetric fracturing design. By optimizing the parameters involved in volumetric fracturing simulation using numerical simulation technology, we aimed to maximize its effectiveness. In order to enhance the specificity and practicability of the numerical simulation design of volumetric fracturing, we conducted extensive simulation experiments to identify the optimal configuration considering various possible parameter combinations, which enriched theoretical knowledge and provided guidance for practical operation. Finally, based on the studied theories and methods (Fig. 1), a highly practical and targeted set of numerical simulation techniques was developed, which was specially designed to address the geological characteristics such as brittleness of reservoir rocks in the studied block, rock mechanics properties including in situ stress analysis, and the development of natural fractures, thus promoting the effective application of volumetric hydraulic fracturing numerical simulation techniques.
Research technological routes.
The extent of multiple cracks in perforated wells.
The complex fracture network of volumetric fractures refers to the simultaneous generation and propagation of multiple radial multi-fractures along the wellbore, forming an interconnected fracture system that spreads independently of each other. This complex fracture network is formed by the combined effect of two dynamic processes: the generation and propagation of multi-fractures in the wellbore.31,32The gradual decrease in pressure difference between different directions in the wellbore facilitates the simultaneous initiation of multiple fractures, while the gradual increase in bottomhole fluid pressure plays an important role in promoting the simultaneous propagation of fractures.
The fracturing well is completed through the drilling process, taking into account the fracturing pressure calculation formula, which takes into account the filtration loss of the fracturing fluid into the formation.
$$P_{f} = \frac{{3\sigma_{h} – \sigma_{v} + \sigma_{t} – \alpha \left( {\frac{1 – 2\nu }{{1 – \nu }}} \right)P_{p} }}{{1 + \phi – \alpha \left( {\frac{1 – 2\nu }{{1 – \nu }}} \right)P_{p} }}$$
(1)
where \(P_{f}\) Formation rupture pressure, MPa. \(\sigma _{h}\) Minimum horizontal principal stress, MPa. \(\sigma_{t}\) is the tensile stress in rock, MPa. \(\sigma _{v}\) is the normal principal stress, MPa. \(\alpha\) The dimensionless Biot coefficient for rocks. \(\nu\) Poisson’s ratio of rocks, dimensionless. \(P_{p}\) Formation pressure, MPa. \(\phi\) Porosity of the formation, %.
The fracture pressure can be calculated using the aforementioned formula and applied to equation (2) to determine the tangential and radial stresses on the wellbore wall under the combined influence of various components. Considering the low tensile strength of rocks, special attention should be paid to the tangential stresses exerted on the wellbore.33.
$$\left\{ {\begin{array}{*{20}l} {\sigma_{r} = P_{w} – \delta \phi \left( {P_{w} – P_{p} } \right)} \hfill \\ {\sigma_{\theta } = – P_{w} + \delta \left[ {\frac{{\alpha \left( {1 – 2\nu } \right)}}{1 – \nu } – \phi } \right]\left( {P_{w} – P_{p} } \right) + \sigma_{xx} \left( {1 – 2\cos 2\theta } \right) + \sigma_{yy} \left( {1 + 2\cos 2\theta } \right) – 4\tau_{xy} \sin 2\theta } \hfill \\ {\sigma_{z} = \delta \left[ {\frac{{\alpha \left( {1 – 2\nu } \right)}}{1 – \nu } – \phi } \right]\left( {P_{w} – P_{p} } \right) + \sigma_{zz} – \nu \left[ {2\left( {\sigma_{xx} – \sigma_{yy} } \right)\cos 2\theta + 4\tau_{xy} \sin 2\theta } \right]} \hfill \\ {\tau_{r\theta } = 0} \hfill \\ {\tau_{rz} = 0} \hfill \\ {\tau_{\theta z} = – 2\tau_{xz} + 2\tau_{yz} \cos \theta } \hfill \\ \end{array} } \right.$$
(2)
where \(\sigma_{r}\), \(\sigma_{\theta }\), \(\sigma _{z}\) are the normal stress components in the polar-scale system, respectively, in MPa. \(\sigma_{xx}\), \(\sigma_{yy}\), \(\sigma_{zz}\) are the normal stress components (MPa) in the coordinate system (x, y, z), respectively. \(\tau_{r\theta }\), \(\tau_{rz}\), \(\tau_{\theta z}\) are the shear stress components in the polar-scale system, respectively, in MPa. \(P_{w}\) Bottom hole pressure, MPa. \(P_{p}\) Formation pressure, MPa. \(\theta\) Drilling azimuth angle, °.
According to the failure criteria for permeable well walls: \(\sigma_{min} – \alpha P_{p} = – T\)the conditions necessary for the initiation of well wall failure can be derived.
where \(\sigma_{min}\) Minimum tensile stress, MPa. \(\alpha\) The dimensionless Biot coefficient for rocks. \(T\) The tensile strength of rock, MPa.
The effectiveness of fracturing is directly affected by the drilling parameters, as demonstrated by both laboratory experiments and field applications. The distribution of in situ stress after drilling was investigated using the theory of elastic mechanics (Figure 2). The results revealed that the fracture width is affected by the direction, density and diameter of the perforations. An optimal drilling direction exists based on the specific formation and wellbore conditions. Therefore, optimizing the fracturing effect of a perforated well requires integrating the optimization of both the drilling parameters and the fracturing parameters.

In-situ stress distribution in the well34.
In Figure 3, the horizontal axis represents the angle between the line connecting the wellbore circumference and the center of the wellbore and the maximum horizontal principal stress, and the vertical axis represents the tangential stress of the wellbore wall. If the wellhead pressure is limited to 100 MPa and the maximum pumping displacement during fracture stimulation is limited to 18.0 m,3At 1000/min, it is important that the maximum stress in the wellbore wall does not exceed 70 MPa, otherwise cracks will be difficult to initiate. Analysis of Figure 2 shows that the points along the wellbore circumference most likely to initiate near-wellbore cracks are those with angles of 0° or 180°.

Prediction of tangential force distribution around the well.
Horizontal principal stress analysis
The path of hydraulic fractures away from the wellbore is mainly determined by the distribution of the in situ stress field far from the wellbore. One of the factors that most influence the formation of fracture networks is the difference in in situ stress levels. If this difference is too large, it is difficult to establish a fracture network with large dimensions. Even in that case, only simple double-wing fractures will be formed. Therefore, it is important to investigate the in situ stress state of each individual wellbore. The distribution of the in situ stress field can be calculated using a formula commonly used to determine the maximum and minimum horizontal principal stresses.
$$\left\{ {\begin{array}{*{20}c} {\sigma_{h} = \left( {\frac{\nu }{1 – \nu } + \beta_{1} } \right) \times \left( {\sigma_{v} – \alpha P_{p} } \right) + \alpha P_{p} } \\ {\sigma_{H} = \left( {\frac{\nu }{1 – \nu } + \beta_{2} } \right) \times \left( {\sigma_{v} – \alpha P_{p} } \right) + \alpha P_{p} } \\ \end{array} } \right.$$
(3)
where \(\alpha\), \(\beta\) It is a coefficient related to the actual reservoir block and is obtained from previous fracturing data. \(P_{p}\) Formation pore water pressure, MPa. \(\nu\) It is the Poisson’s ratio of the rock and is dimensionless.
After analyzing more than 40 wells, it was found that the stress differentials in this area are typically in the range of 3.5–8.7 MPa, which is relatively small. Therefore, it can be inferred that the feasibility of the volumetric fracturing method is high.
Degree of natural crack development
An important factor in matrix fracturing is the degree of natural fracture development in the vicinity of the wellbore. The more developed these pre-existing fractures are, the more likely they are to be induced by multi-stage fracturing, which results in fracture propagation and ultimately leads to the formation of a complex fracture network. The appearance of rock cores extracted from underground reservoirs was described, and statistical methods were used to analyze the natural fracture development characteristics of the target formation (Table 1). It is clear that the density of naturally occurring fractures in the vicinity of the wellbore is consistently greater than 2.0/m, indicating a significant increase in the level of fracture development throughout the block. This significant degree of development significantly facilitates the creation of a complex fracture network by hydraulic fracturing.35,36.
Rock Brittleness Index
Rickman et al.37 A rapid rock brittleness assessment method that can be directly applied in the field is introduced.
$$B_{rick} = \frac{{\left( {E_{G} + \nu_{G} } \right)}}{2}$$
(Four)
$$\left\{ \begin{gathered} E_{G} = \frac{{100(E – E_{\min } )}}{{E_{\max } – E_{\min } }} \hfill \\ \nu_{G} = \frac{{100(\nu – \nu_{\max } )}}{{\nu_{\min } – \nu_{\max } }} \hfill \\ \end{gathered} \right.$$
(5)
where \(for example}\) Normalized Young’s modulus, dimensionless. \(\nu_{G}\) The normalized Poisson’s ratio, which is dimensionless. \(E_{min}\), \(E_{max}\) The minimum and maximum Young’s modulus in the block, in GPa. \(\nu_{min}\), \(\nu_{max}\) The minimum and maximum Poisson’s ratio in the block (dimensionless). \(B_{Rick}\) The Richman Fragility Index.
High rock brittleness characteristic parameters will lead to the extensive development of fracture networks in the reservoir, and the amount of fracturing fluid needs to be increased. However, it is possible to reduce both the concentration and amount of proppant used. By integrating the logging data of more than 30 wells in the X well block and applying equations (4) and (5), the brittleness index of the fractured layers of these wells can be calculated. According to the calculation results shown in Figure 4, most of these wells show rock brittleness index in the range of about 60%, which promotes the formation of multiple fractures in the reservoir and promotes the networked extension of hydraulic fractures.
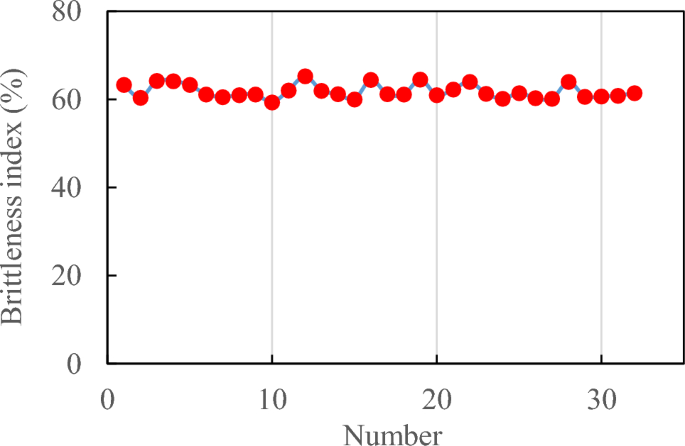
Brittleness index calculated based on rock mechanics parameters.
The higher the brittleness index of a rock, the more likely rock failure will occur and the more developed the resulting fracture network will be. 38When the brittleness index of rocks is 10-20%, bilaterally symmetric cracks are likely to form. When the brittleness index is 30-40%, multiple cracks tend to occur. When the brittleness index is 40-50%, the crack morphology transitions from crack network to multiple cracks. When the brittleness index is greater than 50%, the cracks generated by pressure show a network structure. Based on this analysis, it can be inferred that volumetric fracturing in the reservoirs in the study area is likely to generate a large number of complex and intricate crack networks.